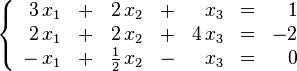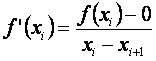SISTEMAS DE ECUACIONES LINEALES

                SISTEMA
                    DE ECUACIONES 
                                       LINALES


Un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones o simplemente sistema lineal, es un conjunto de ecuaciones lineales (es decir, un sistema de ecuaciones en donde cada ecuación es de primer grado), definidas sobre un cuerpo o un anillo periferico. 

Un ejemplo de sistema lineal de ecuaciones sería el siguiente:

             

                        

                MÉTODO
                        DE
                            GAUSS

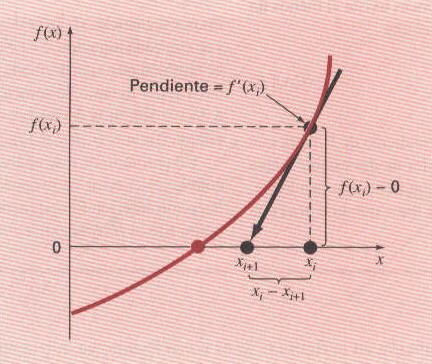
El método de Gauss consiste en transformar un sistema de ecuaciones en otro equivalente de forma que éste sea escalonado.

Para facilitar el cálculo vamos a transformar el sistema en una matriz, en la que pondremos los coeficientes de las variables y los términos independientes (separados por una recta).

 

   

           METODO DE GAUSS JORDAN
                      (matriz inversa)

Dada una matriz A, ¿Podremos encontrar otra matriz B tal que A·B=B·A=I?

Esta matriz B existe aunque no siempre, de existir se le llama matriz inversa de A y se nota A^-1. Para que exista la inversa de A, ésta tiene que ser cuadrada pues de lo contrario no se podría hacer el producto por la izquierda y por la derecha, luego cuando hablamos de matrices invertibles estamos hablando de matrices cuadradas.

Condición necesaria y suficiente para que una matriz sea invertible es que no sea singular, es decir, que su determinante sea no nulo |A| ≠ 0

Cálculo de la matriz inversa
1. Método de Gauss-Jordan

 
Este método consiste en colocar junto a la matriz de partida (A) la matriz identidad (I) y hacer operaciones por filas, afectando esas operaciones tanto a A como a I, con el objeto de transformar la matriz A en la matriz identidad, la matriz resultante de las operaciones sobre I es la inversa de A (A^-1).
Las operaciones que podemos hacer sobre las filas son:
a) Sustituir una fila por ella multiplicada por una constante, por ejemplo, sustituimos la fila 2 por ella multiplicada por 3.
b) Permutar dos filas
c) Sustituir una fila por una combinación lineal de ella y otras.

2. A través de la matriz de adjuntos

Dada una matriz A, determinamos la matriz de adjuntos de su traspuesta. Si multiplicamos esa matriz por 1/|A| se obtiene la matriz inversa de A.

                       

METODO DE EULER

     MÉTODO
                   DE 
                       EULER 

En el método de Euler se tomó como válida para todo el intervalo la derivada encontrada en   un extremo de éste Fig. 

Para obtener una exactitud ra­zonable se utiliza un intervalo muy pequeño, a cambio de un error de redondeo mayor (ya que se realizarán más cálculos).

El método de Euler modificado trata de evitar este problema utilizando un valor promedio de la derivada tomada en los dos extremos del intervalo. en lugar de la derivada tomada en un solo extremo.

  EL MÉTODO DE EULER MODIFICADO:

1. Se parte de (xo,Yo) Y se utiliza el método de Euler a fin de calcular el valor de Y correspondiente a Xl' Este valor de Y se denotará aquí como YI' ya que sólo es un valor transitorio para Yl' Esta parte del proceso se conoce como paso predictor.

2. El segundo paso se llama corrector, pues trata de corregir la predicción. En el nuevo punto obtenido (XI, Yl) se evalúa la derivada [(xI' YI) usando la ecua­ción diferencial ordinaria del PVI que se esté resolviendo; se obtiene la media aritmética de esta derivada y la derivada en el punto inicial (xo' Yo)

1/2 [F(xo ,Yo) + F(Xl,YI)] = derivada promedio

Se usa la derivada promedio para calcular un nuevo valor de y₁, con la ecuación y₁=y₀+hf(x₀,y₀), que deberá ser mas exacto que y₁

y se tomara como valor definitivo de y₁. Este procedimiento se repite hasta llegar a y_n.

El esquema iterativo para este método  quedara en general así:

Primero, usando el paso de predicción resulta:

 

.

Una vez obtenida y_i+1 se calcula f(x_i+1,y_i+1), la derivada en el punto (x_i+1,y_i+1), y se promedia con la derivada previa (x_i,y_i) para encontrar la derivada promedio

Se sustituye f(x_i,y_i) con este valor promedio en la ecuación de iteración de euler y se obtiene:

euler



programa en c++

RAICES DE ECUACIONES

TEOREMA 

                  FUNDAMENTAL 

                                              DEL 

                                                       ALGEBRA

El Teorema Fundamental del Álgebra (TFA) dice que todo polinomio a coeficientes complejos tiene una raíz compleja, es decir existe un número complejo donde el polinomio evalúa a cero. Hay muchas demostraciones de este importante resultado. Todas requieren bastantes conocimientos matemáticos para formalizarlas. Sin embargo, si se deja de lado algo del rigor matemático, hay argumentos simples y creíbles, que le permiten a uno convencerse de la veracidad del TFA. Nuestro objetivo es presentar a continuación uno de estos argumentos

http://enciclopedia.us.es/index.php/Teorema_fundamental_del_%C3%A1lgebra

  REGLA
                DE LOS 
                               SIGNOS 
                                              DE 
                                                    DESCARTES 


*Dice: El número de raíces Positivas es igual al número de variaciones de f(x) ó es menor que este número en un número par.

*Dice: El número de raíces Negativas es igual al número de variaciones de f(-x) ó es menor que este número en un número par.

Por Ejemplo:

2x^5+3x^4-2x^2+x-2

Positivos: 3 Negativos: 2 imaginarios: 0

La regla de los signos de descartes nos dice de acuerdo con la tabla anterior que la ecuación tiene por lo menos una Raíz Positiva y Máximo 3, y que ó tiene 2 Raíces Negativas ó no tiene ninguna.

            MÉTODO
                            DE
                                NEWTON-RAPHSON

Entre los métodos de aproximaciones sucesivas para encontrar algunas de las raíces de una ecuacíon algebraica o tracendente, el de Newton-Raphson es el que presenta mejores características de eficiencia, debido a que casi siempre converge a la solución y lo hace en un número reducido de iteraciónes.

         

Este método es aplicable tanto en ecuaciones algebraicas como tracendentes y con él es posible obtener raíces complejas.

        

Tal vez, de las fórmulas para localizar raíces, la fórmula de Newton-Raphson sea la más ampliamente utilizada. Si el valor inicial para la raíz es xi, entonces se puede trazar una tangente desde el punto [xi,f(xi)] de la curva. por lo común, el punto donde esta tangente cruza el eje x representa una aproximación mejorada de la raíz.

El método de Newton-Rapshon se deduce a partir de esta interpretación geométrica.

El método de Newton-Raphson, como todos los de aproximaciones sucesivas, parte de una primera aproximación y mediante la aplicación de una formula de recurrencia se acercara a la raíz buscada, de tal manera que la nueva aproximación se localiza en la interseccíon de la tangente a la curva de la función en el punto y el eje de las abscisas.

De la figura se tiene que la primer derivada en x es equivalente a la pendiente:

que se reordena para obtener:

la cual se conoce como fórmula de Newton-Raphson.

SERIES DE TAYLOR Y MC LAURIN

SERIE DE TAYLOR

La serie de Taylor se basa en ir haciendo operaciones según una ecuación general y mientras mas operaciones tenga la serie mas exacto será el resultado que se esta buscando. Dicha ecuación es la siguiente:

o expresado de otra forma





Donde n! es el factorial de n
F(n) es la enésima derivada de f en el punto a


Como se puede observar en la ecuación, hay una parte en la cual hay que desarrollar un binomio (x-a) n por lo que para simplificar el asunto se igualara a "a" siempre a 0. Para fines prácticos no afecta mucho en el resultado si se hacen muchas operaciones en la serie.


SERIE DE MC LAURIN

En matemáticas, la serie de Taylor de una función f(x) infinitamente derivable (real o compleja) definida en un intervalo abierto (a-r, a+r) se define con la siguiente suma: sin(x) y aproximaciones de Taylor centradas en 0, con polinomios de grado 1, 3, 5, 7, 9, 11 y 13.

f(x) = \sum_{n=0}^{\infin} \frac{f^(n)(a)}{n!} (x-a)^{n} 


Aquí, n! es el factorial n y f (n)(a) indica la n-ésima derivada de f en el punto a.

Si esta serie converge para todo x perteneciente al intervalo (a-r, a+r) y la suma es igual a f(x), entonces la función f(x) se llama analítica. Para comprobar si la serie converge a f(x), se suele utilizar una estimación del resto del teorema de Taylor. Una función es analítica si y solo si se puede representar con una serie de potencias; los coeficientes de esa serie son necesariamente los determinados en la fórmula de la serie de Taylor. Si a = 0, a la serie se le llama serie de Maclaurin.

Esta representación tiene tres ventajas importantes:

* La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.

 * Se puede utilizar para calcular valores aproximados de la función.

* Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible. 

ANÁLISIS DE ERRORES Y GRAFICACIÓN

•  TIPOS DE ERRORES
  
  

  EXACTITUD Y PRECISIÓN

  
  

  Los errores asociados con los cálculos y medidas se pueden caracterizar observando su precisión y exactitud. La precisión se refiere a 1) el numero de cifras significativas que representa una cantidad o 2) la extensión en las lecturas repetidas de un instrumento que mide alguna propiedad física. La exactitud se refiere a la aproximación de un número o de una medida al valor verdadero que se supone representa.

  
  DEFINICIÓN DE ERROR
  
  

  Los errores numéricos se generan con el uso de aproximaciones para  representar las operaciones y cantidades matemáticas. Esto incluye errores de truncamiento que resultan de representar aproximadamente un procedimiento matematico exacto, y los errores de redondeo, que resultan de presentar aproximadamente números exactos. Para los tipos de errores, la relación entre el resultado exacto o verdadero y el aproximado esta dado por :

  
  Valor verdadero = valor aproximado + error ( Ec.1 )
  
  

  Reordenando la ecuación Ec.1, se encuentra que el error numérico es igual a la diferencia entre el valor verdadero y el valor aproximado esto es :

  
  

  Ev = valor verdadero – valor aproximado
  
  

  Donde Ev se usa para redondear el valor exacto del error. Se incluye el subíndice v par dar a entender que se trata del “verdadero” error. Un defecto es que muchas veces no se toma en consideración el orden de

  magnitud del valor que se esta probando . Por ejemplo, un error de un centímetro es mucho mas significativo si se esta midiendo un remache que un puente. Una manera de medir las magnitudes de las cantidades que se

  están evaluendo es normalizar el error respecto al valor verdadero, como en:

  
  Error relativo fraccional = error / valor verdadero
  
  Donde: Error = valor verdadero – valor aproximado.
  
  El error relativo también se puede multiplicar por el 100% para expresarlo como:
  
   Ev = (error verdadero/ valor verdadero ) 100
  
  

  Donde Ev denota el error relativo porcentual. El subíndice v significa la normalización del error al valor verdadero . Para los métodos numéricos el valor verdadero únicamente se conocerá cuando se habla de funciones que se pueden resolver analíticamente. Sin embargo, en aplicaciones reales, no se conoce la respuesta verdadera. En estos casos, normalizar el error es una alternativa usando la mejor estimación posible del valor verdadero, esto es a la aproximación misma, como:

  
  Ea = (error aproximado/ valor aproximado)100
  
  

  Donde el subíndice a significa que el error está normalizado a un valor aproximado .Uno de los retos a que se enfrentas los métodos numéricos es el de determinar estimaciones del error en ausencia de conocimiento de los valores verdaderos. El error se calcula como la diferencia entre la aproximación previa y la actual. Por lo tanto, el error relativo porcentual está dado por:

  
  Ea =abs( ((aproximación actual- aproximación previa )/ aproximación actual) 100)
  
  

  Si se cumple la relación anterior , entonces se considera que el resultado obtenido esta dentro del nivel aceptable, es decir, aun error previamente fijado.